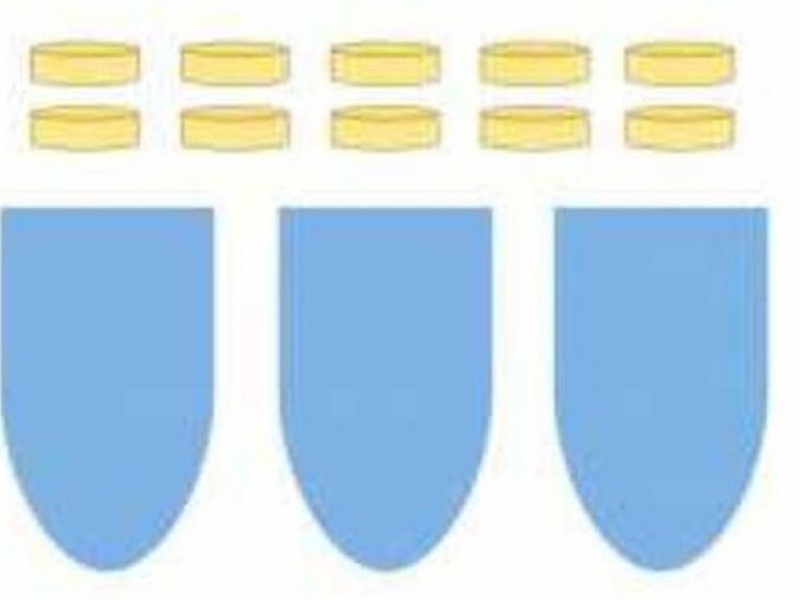
Можете ли да поставите 10 монети в 3 чаши, така че всяка чаша да съдържа нечетен брой монети? Това е загадка, която някои компании задават по време на интервю за работа, пише "Петел".
Пробвайте се!
Съвет: Мислете креативно!

Съществуват няколко възможни комбинации от положителни числа, чийто сбор дава 10:
1 + 1 + 8
1 + 2 + 7
1 + 3 + 6
1 + 4 + 5
2 + 2 + 6
2 + 3 + 5
2 + 4 + 4
3 + 3 + 4
Обърнете внимание, че най-малко едно от числата в комбинациите е четно. Това означава, че не е възможно да поставим нечетен брой монети във всяка една от трите чаши.
Казано иначе, ако в чашите има нечетен брой монети 2x + 1, 2y + 1 и 2z + 1, то за да получим сбор от 10, трябва да имаме:
(2x + 1) + (2y + 1) + (2z + 1) = 10
Това означава:
2(x + y + z) = 7
Няма как да имаме два пъти положително число, равно на 7. Затова трябва да мислим креативно.
Да вземем разделението 2 + 3 + 5. Сега – нека поставим средната чаша с 3 монети в първата чаша с 2. Вече всяка чаша съдържа нечетен брой монети.

Естествено, решението работи и с други комбинации от числа, в които имаме 2 нечетни числа и 1 четно.
Можем да изберем и да не слагаме каквито и да е монети в първата чаша.
0, 1, 9
0, 3, 7
0, 5, 5
След това е достатъчно да поставим една от чашите с нечетен брой монети върху тази с 0.
TNS.bg
Още от категорията
Виж всички
Митът за ранното ставане и истината за продуктивността

















